 Reprezentacja Polski w piłce nożnej nie będzie w grupie ani z Anglią, ani z Hiszpanią, ale i tak nasze towarzystwo tworzy „grupę śmierci”. Awans do dalszej części turniej będzie bardzo trudny. Aby to stwierdzić nie trzeba pytać wróża Macieja ani jasnowidza Jackowskiego. Wystarczą proste narzędzia statystyczne. Proszę nie udostępniać tego tekstu naszym reprezentantom, bo to co przeczytacie dalej, może ich poważnie zestresować.
Reprezentacja Polski w piłce nożnej nie będzie w grupie ani z Anglią, ani z Hiszpanią, ale i tak nasze towarzystwo tworzy „grupę śmierci”. Awans do dalszej części turniej będzie bardzo trudny. Aby to stwierdzić nie trzeba pytać wróża Macieja ani jasnowidza Jackowskiego. Wystarczą proste narzędzia statystyczne. Proszę nie udostępniać tego tekstu naszym reprezentantom, bo to co przeczytacie dalej, może ich poważnie zestresować.
Mam nieodparte wrażenie, że większość kibiców piłki nożnej w naszym kraju jest zaniepokojona wynikami losowania grup Mistrzostw Świata Rosja 2018. Balonik był dmuchany właściwie już od zakończenia Mistrzostw Europy, a okazało się że nawet bez rozegrania jednego meczu na MŚ, oczekiwania zostały mocno przytłumione i zamiast marzyć o Pucharze zaczynamy obawiać się o wyjście z grupy. Teoretycznie nie trafiliśmy najgorzej. Przecież nie ma w naszej grupie ani Hiszpanii, ani Anglii, a jednak rewizja oczekiwań wydaje się jak najbardziej uzasadniona.
Pomyślałem zatem o przeprowadzeniu małej zabawy statystycznej, która pomoże zrozumieć zmianę nastrojów. Nie będę w tym miejscu tworzył pełnego modelu probabilistycznego, a jedynie wykorzystam elementy statystyki. Dlatego też swoje rozważania nazywam bardziej zabawą niż analizą, niemniej jednak pokuszę się o argumentację tez, które przedstawię. Mam nadzieję, choć w drobny sposób przybliżę części czytelników proces tworzenia modeli analitycznych przeróżnych zjawisk, jakie są przedmiotem naszej codziennej pracy. Jeśli podążycie ze mną w głąb niniejszego artykułu, znajdziecie odpowiedź na pytanie jak można porównać trudność poszczególnych grup i czy o polskiej grupie można mówić rzeczywiście „grupa śmierci”.
Jak określić „trudność” grupy na MŚ?
Przed rozpoczęciem analizy dowolnego zagadnienia wypada je poprawnie zdefiniować. Zatem zastanówmy się jak można określić „trudność” poszczególnych grup, tak aby móc dokonać oceny na podstawie choćby uproszczonego modelu statystycznego? Najbardziej naturalnym pomysłem wydaje się ustalenie „siły” każdej grupy na podstawie rankingu odzwierciedlającego jakość piłkarską, a następnie ich uszeregowanie od najwyższej do najniższej. Możemy przyjąć jako miarę „siły” wartość średnią z punktów rankingowych. Tylko czy tak określona „siła” pozwoli na odpowiedź na pytanie jak trudno będzie wyjść z danej grupy? Dla przykładu możemy mieć w grupie dwie bardzo silne drużyny i dwie bardzo słabe. Wartość średnia punktów rankingowych może być znacząca, jednak z wysokim prawdopodobieństwem możemy określić kto wyjdzie z danej grupy. Zatem czy o takiej grupie można powiedzieć, że jest „trudna”? Na pewno dla najsłabszych drużyn tak, ale dla najmocniejszych… raczej niespecjalnie.
W moim odczuciu o „trudności” grupy stanowi to, na ile trafnie możemy określić, kto zdoła z danej grupy awansować do dalszych rozgrywek. W tym celu chciałbym porównać jak bardzo oddalone pod względem jakości piłkarskiej są od siebie drużyny w każdej grupie. Im będą od siebie bardziej oddalone, tym bardziej prawdopodobne będzie właściwe przewidzenie drużyn które awansują. A z kolei im drużyny będą do siebie bardziej zbliżone poziomem piłkarskim, tym trudniej przewidzieć kto awansuje dalej.
Jakość piłkarska / Ranking Elo
Do porównania jakości piłkarskiej reprezentacji wybrałem ranking Elo. W mojej ocenie jest on zdecydowanie bardziej sprawiedliwy niż ranking FIFA, który opiera się na średniej ilości punktów za mecze rozegrane w ostatnich 12 miesiącach. Nie wchodząc zbytnio w szczegóły, każdy rozegrany mecz towarzyski powoduje w przypadku silnych drużyn spadek liczby punktów. Bez względu na wynik. Oczywiście wygrana zaowocuje mniejszą „karą” niż porażka, ale najlepiej meczy towarzyskich nie rozgrywać. Doskonale obrazuje to przykład reprezentacji Polski w ostatnim roku. Zresztą taką samą „sztuczkę” wykonała Belgia przed poprzednim Mundialem.
Dlaczego zatem ranking Elo jest lepszym wskaźnikiem jakości piłkarskiej? Przede wszystkim opiera się na sumie punktów, a nie na średniej. W efekcie każda wygrana, nawet w meczu towarzyskim, podnosi ranking zespołu, a każda porażka obniża. Oczywiście są odpowiednie wagi, które biorą pod uwagę rangę spotkania, miejsce rozgrywania i różnicę w pozycjach rankingowych.
Wariancja, odchylenie standardowe – ta straszna statystyka
Kluczowym założeniem całej analizy, jest kwestia uznania, że ranking Elo dokładnie oddaje jakość piłkarską danej ekipy. Oczywiście można tą tezę obalić na 1000 sposobów, ale na potrzeby poniższej zabawy uznam to przybliżenie za wiarygodne.
Wybór odpowiedniej miary jakości piłkarskiej to połowa sukcesu. Za drugą odpowiada wybór odpowiedniego parametru do zmierzenia oraz jego prawidłowa estymacja. Wiem, to brzmi trochę złowrogo, ale już spieszę z wyjaśnieniem.
Chcąc porównać jak bardzo oddalone są od siebie reprezentacje w poszczególnych grupach, zmierzyłem odchylenie standardowe rankingu Elo w każdej z grup. W celu obliczenia wartości odchylenia standardowego użyłem estymatora s:
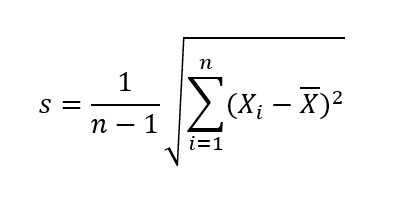
Gdzie:
Xi – wartość rankingu Elo i-tej drużyny w danej grupie
X – wartość średnia rankingu Elo w danej grupie
n – liczba drużyn w danej grupie (zawsze równa 4)
Wszystko jasne, prawda? 😛 Nadchodzi upragniona pomoc. Odchylenie standardowe pokazuje nam jak bardzo oddalone są obserwacje od średniego poziomu w danej grupie. Będzie tym mniejsze im drużyny będą bliżej siebie w rankingu i tym większe im drużyny będą od siebie dalej. W efekcie im mniejsze odchylenie standardowe, tym bardziej wyrównany poziom grupy i tym trudniej przewidzieć drużyny, które awansują do dalszych rozgrywek.
Przykład dla niewtajemniczonych
Jeśli chcesz dokładniej sprawdzić jak działa odchylenie standardowe, poniżej znajdziesz pomocny przykład.
Załóżmy, że mamy 3 drużyny o A, B i C odpowiednio o rankingu 10, 5, 0. Wtedy wartość średnia rankingu wynosi (10 + 5 + 0)/3 = 5. Podstawiając do wzoru na odchylenie standardowe otrzymamy:
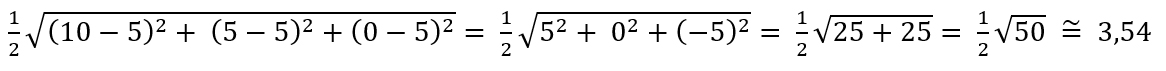
Dla porównania sprawdźmy wynik dla 3 drużyn X, Y, Z odpowiednio o rankingu 7, 5, 3. Wtedy wartość średnia rankingu również wynosi 5 = (7 + 5 + 3)/3. A ile wyniesie odchylenie standardowe? Sprawdzamy:
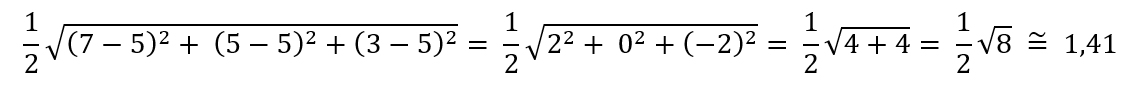
Jak widać zaproponowane podejście zdaje egzamin i dla drużyn o bardziej wyrównanym poziomie odchylenie standardowe jest zdecydowanie mniejsze.
To jaki jest ten wyniki?
Dość tej teorii, pora pokazać efekty. Poniżej znajdziecie wyniki dla każdej grupy. Każdy kraj ma przypisaną odpowiednią wartość rankingu Elo według stanu na 4 grudnia 2017. W każdej grupie została pokazana średnia z rankingu Elo oraz odchylenie standardowe.

Która grupa na mistrzostwach jest „grupą śmierci”?
Dla ułatwienia poniżej uszeregowałem grupy według wartości odchylenia standardowego:
1. Grupa H – 81 (Polska, Senegal, Kolumbia, Japonia)
2. Grupa C – 104 (Francja, Australia, Peru, Dania)
3. Grupa A – 109 (Rosja, Arabia Saudyjska, Egipt, Urugwaj)
4. Grupa D – 114 (Argentyna, Islandia, Chorwacja, Nigeria)
5. Grupa B – 155 (Portugalia, Hiszpania, Maroko, Iran)
6. Grupa G – 159 (Belgia, Panama, Tunezja, Anglia)
7. Grupa F – 164 (Niemcy, Meksyk, Szwecja, Korea Płd.)
8. Grupa E – 168 (Brazylia, Szwajcaria, Kostaryka, Serbia)
Wynik przeprowadzonej analizy wskazuje, że najbardziej wyrównaną jest grupa polska. O awans może walczyć każdy i nie ma zdecydowanego faworyta. Zatem nazywając rzeczy po imieniu, to nasza grupa jest „grupą śmierci”. Ciekawie powinno być też w grupach C, A i D. Natomiast w grupie G Niemcy i Brazylia właściwie mogą szykować się prosto do drugiej rundy, przynajmniej na podstawie uproszczonego modelu statystycznego 🙂
Dla ścisłości należy jeszcze powiedzieć, że według algorytmu Elo, drużyna rozgrywająca mecz na swoim terenie dostaje premię do oczekiwanego wyniku danego spotkania w wysokości 100 punktów. Czyli uwzględniając tą kwestię w analizie, grupa A powinna mieć nieco inne statystyki:
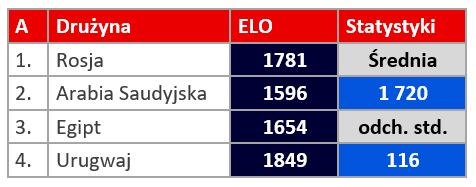
Jak widać wprowadzenie premii za rozgrywanie meczów na własnym boisku, w tym wypadku nie powoduje znaczącej różnicy. Mimo to patrząc na samą wartość punktów rankingowych, ujęcie tej premii lepiej odzwierciedla siłę w grupie.
Jak dobra jest moja analiza?
Zaprezentowana analiza nie jest idealna. Przede wszystkim dlatego, że odnosi się do całości grupy, a nie do poszczególnych drużyn. Jednak należy jej oddać, że jest prosta, szybka do przeprowadzenia i pozwala wyciągnąć pierwsze wnioski, które pokrywają się z odczuciami. Zatem jest jak najbardziej na miejscu i według mnie stanowi dobry wybór jako pierwsze porównanie. Przy rozwiązywaniu problemu zawodowego i stworzenia dokładnego modelu, w pierwszym podejściu skorzystałbym z takiej właśnie analizy, aby poznać ogólną sytuację.
Natomiast jeśli miałbym rozważyć szczegółowo zagadnienie określenia szansy każdej drużyny, czy to na awans do kolejnej rundy, czy osiągnięcie sukcesu, zdecydowałbym się budować o wiele dokładniejszy model. Jeśli jesteście zainteresowani śledźcie naszego bloga. Jest szansa, że wkrótce taki materiał się pojawi.


